On Fri, 3 Nov 2000, a complete unknown sent me the following mathematical/mechanical problem, and I still don't know how the person could guess that I ever had education which allowed me to solve problems like this. But anyway, having ample spare time at that time, I solved the problem and sent it back to sender. Just for the interested, here it is...
> CONSIDER A CAR WITH 10 ' AXLES. SUPPOSE THAT THE CAR IS DRIVING AROUND A
> CIRCLE, W/ RADIUS 30' AT A SPEED OF ONLY 10 m.p.h. ASSUMING THAT THE CAR'S
> WHEELS (w/tires mounted) HAVE A RADIUS EQUAL TO 8", FIND THE rpm OF BOTH
> THE INSIDE AND THE OUTSIDE WHEELS/TIRES.
Mind that I'm used to calculate in metric units, like most people in Europe. This is also necessary to make the formulas work out. So I'll convert distances in feet and inches to meters, and velocities in m.p.h. to meters/second via the following factors:
1' = 0.3048 m
1" = 0.0254 m
1 m.p.h. = 0.447 m/s
In general, the velocity of a point, rotating at an angular velocity w, is equal to v = r * w, where r is the distance (radius) to the center of rotation. This is logical: points on the edge of a rotating disc move faster than points in the middle (and the center of the disc doesn't move at all). w is expressed in radians per second, and there are 2 * p (= 2 * 3.1416) radians in a full circle.
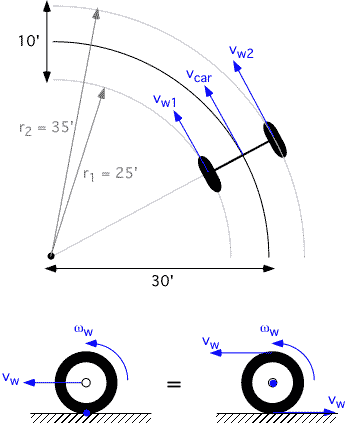 The car moves at 10 m.p.h., so 4.4704 m/s. I assume that it's the center of the car which moves at this velocity, and that this center is on the circle of radius 30' = 9.144m. Its angular velocity can now be calculated by dividing both sides of the above formula by r, which gives:
The car moves at 10 m.p.h., so 4.4704 m/s. I assume that it's the center of the car which moves at this velocity, and that this center is on the circle of radius 30' = 9.144m. Its angular velocity can now be calculated by dividing both sides of the above formula by r, which gives:
w = v/r
Filling in the numbers:
w = 4.47 / 9.144 = .489 rads/sec
Now we also know the angular velocity of both wheels, which is exactly the same, as the whole car is rotating around the same point. So we can calculate the linear speed of both wheels by multiplying w by both distances from the rotation point, which are 25' = 7.62m and 35' = 10.67m
vw1 = w * 7.62 = 3.73 m/s
vw2 = w * 10.67m = 5.22 m/s
As you can see, the inner wheel moves slower than the middle of the car, which moves slower than the outer wheel.
Now comes the trickiest part: viewed from outside the car, from a momentarily point of view, the wheels rotate around their contact points with the ground (left image below). However, if you look at the situation from inside the car, it is the floor which moves and the axle which stands still (right image below). Of course we are only interested in what we see from inside the car. We use the same formula:
w = v/r,
and r is the radius of the wheel = 8" = 0.203m
So for the inner wheel: ww1 = 3.73 / 0.203 = 18.3 rad/s
And for the outer wheel: ww2 = 5.22 / 0.203 = 25.7 rad/s
But the angular velocity of both wheels was asked in rounds per minute. There are 60 seconds in one minute, so one rad/s equals 60 rads per minute. There is one round in two*p radians, so one rad/s equals 60/(2*p) rounds per minute. So we simply have to multiply our results by 60/(2*3.1416) = 9.55
So for wheel 1, the rpm = 245 rounds per minute
And for wheel 2, the rpm = 175 rounds per minute.
Surprisingly or not, you would get the same results when considering the first point of view, i.e. outside the car. You would need to use 2*8" 16" for r, and 2*vw for v. And when dividing these both numbers by each other, the factor 2 vanishes again, as 2/2 = 1.
I hope this makes things clear!
Alexander Thomas
 The car moves at 10 m.p.h., so 4.4704 m/s. I assume that it's the center of the car which moves at this velocity, and that this center is on the circle of radius 30' = 9.144m. Its angular velocity can now be calculated by dividing both sides of the above formula by r, which gives:
The car moves at 10 m.p.h., so 4.4704 m/s. I assume that it's the center of the car which moves at this velocity, and that this center is on the circle of radius 30' = 9.144m. Its angular velocity can now be calculated by dividing both sides of the above formula by r, which gives: